全部分类/
教育教学/
高中数理化

高中数理化

2024年21期

北师大集团核心刊物

扫码免费借阅

目录

快速导航

高考　课改 | 优化运算技巧　溯源体现本质

高考　课改 | 优化运算技巧　溯源体现本质

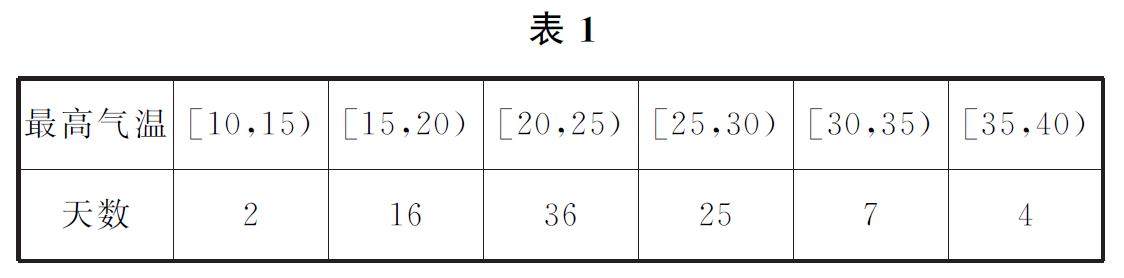
新高考实施以来更加关注对高阶思维的考查，落实创新性的考查要求，也更加关注对同一主题下多个知识点的综合考查．而２０２４年新课标Ⅰ卷数学第１６题是一个典型的例子，重点考查数学运算核心素养，注重对数学运算严谨性的考查．考试时学生短时间内既要知道如何运算，还要能够准确运算，因而要想拿满分绝非易事．笔者从不同角度，开拓思路，分析解答，探索运算过程的逐步优化，之后对命题进行了追本溯源，以期发挥高考题的效果与效
高考全关注 | 如何读懂概率题

高考全关注 | 如何读懂概率题

通常概率统计问题题目较长，若题干表达陌生，会让学生产生恐惧心理，此时更加需要数学阅读能力．如何读懂概率题？这需要全面把握题目信息，理解已知条件与待求结果之间的关联，运用所学知识进行深度思考，并用恰当的数学语言表达出来，从而解决问题．在此，本文以随机变量的确定为例，对如何读懂概率题进行探究．１引例探究题目某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶４元，售价每瓶６元，未售
高考全关注 | 多题一解寻通法　回归教材是真谛

高考全关注 | 多题一解寻通法　回归教材是真谛

«普通高中数学课程标准（２０１７年版２０２０年修订）»在学业水平考试与高考命题原则中强调：“考查内容应围绕数学内容主线，聚焦学生对重要数学概念、定理、方法、思想的理解和应用，强调基础性、综合性;注重数学本质、通性通法，淡化解题技巧．”“在命题中，需要突出内容主线和反映数学本质的核心概念、主要结论、通性通法、数学应用和实际应用．”那什么是“通性通法”呢？章建跃博士曾指出：“通性”就是概念所反映的数
高考全关注 | 高考中直线与圆的常见题型分析

高考全关注 | 高考中直线与圆的常见题型分析

直线与圆是高中数学中的基础知识，高考中往往会对二者进行综合考查．通过对历年高考真题进行总结，可以发现相关问题主要集中在直线与圆的基础知识、位置关系及最值求解．相关问题并不复杂，属于学生必拿分题．为提高学生对直线与圆常见考题的掌握，本文结合实际问题进行分析，供读者参考．
题根研究 | ２０２４年高考两道圆锥曲线解题思路的同一及探究

题根研究 | ２０２４年高考两道圆锥曲线解题思路的同一及探究

大部分圆锥曲线解答题第（２）问都蕴含了丰富的背景和一些特殊结论，对这些试题进行背景溯源、解题分析和探究拓展，可以最大化地发展学生的理性思维，提升学生的问题求解能力．本文以两道２０２４年圆锥曲线高考真题为例，深入探究，对一般情况进行推广，得到椭圆中直线过定点或直线斜率为定值的结论，并类比到双曲线和抛物线中．
题根研究 | 一类高考解析几何压轴题的巧解与拓展

题根研究 | 一类高考解析几何压轴题的巧解与拓展

在解析几何中，遇到直线与圆锥曲线相交的几何问题，常规方法是设出直线方程并将其与圆锥曲线方程联立，再运用根与系数的关系解决问题．事实上，这种处理方法往往会带来较大的计算量，从而导致学生出现“有思路、没出路”“望题兴叹”的情况．本质原因是解析几何的核心思想是“数形结合”，是运用代数的方法解决几何问题，在解题过程中涉及“数”与“形”的灵活转换和整合．因此，运算便成了问题解决过程中的“拦路虎”．本文通过
考题分类评析 | 聚焦动点到动点距离最值问题

考题分类评析 | 聚焦动点到动点距离最值问题

在解析几何中距离问题很常见，高考中经常会出现一类与动点有关的距离最值问题，如动点到定点的距离最值问题、动点到定直线的距离最值问题和动点到动点的距离最值问题．前两种距离最值问题的求解大都有章可循，难度不大，但对于动点到动点的距离最值问题，学生普遍感到棘手．那么对于这类最值问题，有哪些基本解题思路与解题策略呢？本文结合具体例子和大家谈谈，希望能起到抛砖引玉的作用．
考题分类评析 | 善用几何特征巧解渐近线问题

考题分类评析 | 善用几何特征巧解渐近线问题

双曲线作为圆锥曲线中的一大重点，历年来在高考中都占据了重要地位，其中，渐近线这一特殊元素尤为引人注目．它不仅仅是双曲线图像变化趋势的直观体现，更是解题过程中常用的切入点和桥梁．本文展示如何将题型与考点相结合，引导学生及时进行解题反思，将特殊情况一般化，探寻题目中的隐含规律，建立数学模型，提高解题能力．
考题分类评析 | 例析圆中最值问题的求解方法

考题分类评析 | 例析圆中最值问题的求解方法

圆是近乎完美的平面几何图形，圆中的最值问题是考试的常考点，求解圆中的最值问题有哪些方法和路径呢？以下笔者结合一些例题进行分析探讨．
考题分类评析 | 椭圆离心率的取值范围问题解法探究

考题分类评析 | 椭圆离心率的取值范围问题解法探究

椭圆的离心率是椭圆的几何性质之一，它是用来描述椭圆“扁平”程度的．考试中经常会出现求椭圆离心率的值或取值范围的问题，求椭圆离心率的值，关键是建立含有a，b，c 的方程;而求椭圆离心率的取值范围，关键是建立含有a，b，c 的不等式．本文就椭圆离心率的取值范围问题，谈谈如何寻找题目中的不等关系．
考题分类评析 | 圆锥曲线中平面向量的功能探究

考题分类评析 | 圆锥曲线中平面向量的功能探究

处理圆锥曲线问题的核心方法是将几何问题代数化，代数化的途径是利用坐标法，将形的关系转化为数的运算，而平面向量既有形的直观，又有数的特征，其坐标运算恰恰具有将几何问题代数化的功能．因此，应用平面向量解决圆锥曲线问题，其工具性体现得淋漓尽致，使问题的求解变得简捷．下面举例分析几种常见的问题．
考题分类评析 | 圆锥曲线中定点问题的题型及解题策略

考题分类评析 | 圆锥曲线中定点问题的题型及解题策略

圆锥曲线中定点问题是高考中的常考题型，常常将直线、圆及圆锥曲线等知识融合在一起，综合性强、难度大，重点考查数学思想方法的应用，尤其是数学运算、逻辑推理等核心素养．笔者统计了２０１９—２０２４年的高考试题对该考点的考查情况，对此类问题的常规解题策略进行总结，并结合具体试题进行剖析，以期提高学习解决此类问题的能力．探索性问题具有开放性和发散性，涉及知识与方法范围广，对数学能力和数学思想有较高
核心考点 | 探究圆锥曲线的离心率问题

核心考点 | 探究圆锥曲线的离心率问题

圆锥曲线的离心率问题是高中数学的重要知识点之一，且在高考中常考常新，其定义是曲线到定点（焦点）的距离与到定直线（准线）的距离之比．同时，圆锥曲线的离心率也蕴含着丰富的几何性质，其涉及的问题主要有求离心率对应的值、求离心率的取值范围、求与离心率有关的延伸问题．
核心考点 | 关注抛物线中的三类典型切线问题

核心考点 | 关注抛物线中的三类典型切线问题

抛物线是圆锥曲线中的重点内容，与它相关的问题经常充当高考把关题的角色．因此，我们应该对该问题有透彻的研究，这样才能有把握地指导学生进行高考复习．本文所介绍的关于抛物线的切线问题是一类典型的问题，下面对几道典型的例题进行分析探究并点评，旨在探索解题方法，归纳求解思路，供读者赏阅．
核心考点 | 例析直角三角形全等在解析几何中的应用

核心考点 | 例析直角三角形全等在解析几何中的应用

在平面几何中，全等三角形是一个重要的概念，两个全等三角形有许多优美的性质，合理应用全等三角形的性质能解决很多的几何问题．直角三角形是一类特殊的三角形，直角三角形全等不但在平面几何中扮演着重要的角色，而且在解析几何中也有重要的作用．本文结合部分试题，展示直角三角形全等在解析几何中的应用，供大家参考．
核心考点 | 椭圆综合问题的三个入手点

核心考点 | 椭圆综合问题的三个入手点

椭圆综合问题是高考中的难点题型，解题的思维量大、计算烦琐，考生在处理此类问题时，由于条件错综复杂，往往不知从何入手，只会写一些简单的过程而草草收场．本文就解题思路提出三个入手点，供读者参考．
核心考点 | 圆锥曲线中的三点共线问题

核心考点 | 圆锥曲线中的三点共线问题

证明圆锥曲线中的三点共线问题是一种重要的题型，也是一个难点．证明三点共线问题常用方法主要有斜率法和向量法，下面介绍这两种方法的解题步骤及其应用．
核心考点 | 直击解析几何中的垂直关系

核心考点 | 直击解析几何中的垂直关系

在解析几何中，垂直关系是两条直线之间的一种特殊的位置关系．在解题时，我们往往需要对垂直关系进行合理有效转化，那么垂直关系的转化有哪些基本途径呢？本文举例说明．
方法与技巧 | 定比点差法及其应用

方法与技巧 | 定比点差法及其应用

定比点差法最近两年频繁出现在各类试题中，那什么是定比点差法呢？定比点差法的一般原理又是什么呢？它在圆锥曲线中有哪些应用呢？下面就这些问题展开探究．
方法与技巧 | 聚焦向量中双变量的取值范围与最值问题

方法与技巧 | 聚焦向量中双变量的取值范围与最值问题

平面向量是连接代数与几何的“纽带”，求解平面向量问题既要关注它的几何特征，又要关注它的代数特征，因此平面向量问题具有很强的综合性，尤其是向量中双变量的取值范围与最值问题，这类问题常常出现在各级各类的考试题中．那么求解这类问题有哪些技巧呢？
方法与技巧 | 数学解题中隐圆信息的识别

方法与技巧 | 数学解题中隐圆信息的识别

圆是高中数学中平面解析几何的重要组成部分，也是高考命题的重要内容．但很多问题并不直接给出圆的方程，而是需要通过深入探究才能得到的．因此，我们有必要熟悉圆的隐含形式，这样才能迅速识别出圆的信息．
方法与技巧 | 用好图形表征　巧求最值问题

方法与技巧 | 用好图形表征　巧求最值问题

解数学题，关键在于对题意的理解和隐含条件的发现．挖掘题目中的几何背景，能让我们打破思维定式，找到问题的本质，进而从数形结合的角度，快速解决问题．代数中的最值问题是高中数学中较为常见的一类问题，对于这类问题，如果能用好图形表征，那么往往能起到简化解题过程的作用，甚至可以规避繁杂的运算．本文举例说明．
方法与技巧 | 圆锥曲线中角度问题的考查类型及处理策略

方法与技巧 | 圆锥曲线中角度问题的考查类型及处理策略

以圆锥曲线为背景的角度问题是高考或模拟考试中的常考题型，设问方式主要有比较两个角的大小关系、判断角的范围或求角的值等．此类问题的求解除了要把握好处理解析几何问题的核心思想方法外，往往还会涉及平面向量的应用、直线的斜率关系以及三角函数等内容，下面分类例析．
方法与技巧 | 圆锥曲线中定点、定值问题常用解题方法探究

方法与技巧 | 圆锥曲线中定点、定值问题常用解题方法探究

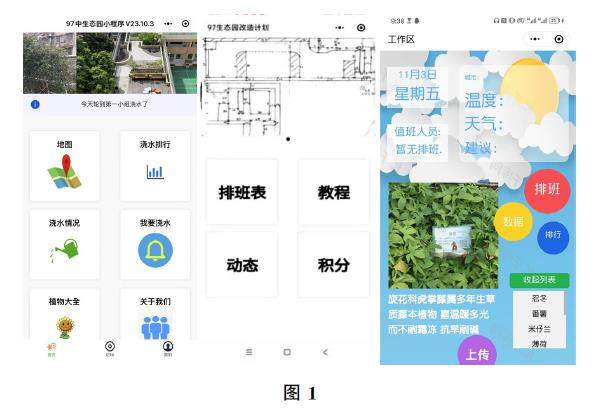
在解析几何问题中，定点、定值问题一直是高考考查的热点，这类问题综合考查学生圆锥曲线的知识储备及计算能力，总体而言难度较高．为提高学生解答定点、定值问题的能力，本文结合实际问题，对几类常用的解题方法进行分析，供读者参考．
教与学 | 人工智能赋能数学建模,实现育人方式的创新

教与学 | 人工智能赋能数学建模,实现育人方式的创新

１引言数学建模作为一种重要的教育活动，在培养学生的数学思维及将数学知识应用于解决实际问题方面发挥着关键作用．«普通高中数学课程标准（２０１７年版）»（以下简称«２０１７版课标»）明确将“数学建模”定位为六大数学学科核心素养的重要组成部分，将“数学建模活动与数学探究活动”纳入高中数学课程的四大核心主线，并着重指出数学建模理念应全面渗透于高中数学教育的每一个环节，由此对数学建模教学实践产生了显著
教与学 | 从教材出发探究一般曲线范围问题的研究方法

教与学 | 从教材出发探究一般曲线范围问题的研究方法

１教材分析人教A 版教材在圆锥曲线的研究过程中，使用数形结合法和坐标法统领全局，始终贯彻“先用几何眼光观察与思考，再用坐标法推理、论证和解决问题”的基本思路．在研究曲线的性质时，教材主要呈现了对范围、对称性、顶点、离心率等性质的研究，本文重点关注曲线范围的研究．教材中通过曲线的方程构造不等关系，研究曲线上点的横坐标与纵坐标的范围，从而得到椭圆的范围，具体研究方法如下．

过往期刊

更多

猜你喜欢

山东政法学院图书馆